Introduction
The aviation industry relies heavily on predictive maintenance to keep operations smooth, safe, and cost-effective. One of the most effective tools for this is survival analysis, which estimates the Remaining Useful Life (RUL) of aircraft engines. Using historical maintenance and failure data, survival analysis can help MRO (Maintenance, Repair, and Overhaul) teams plan proactive maintenance before failures occur, potentially saving costs and improving aircraft uptime. In this article, we will walk through how to use survival analysis with Python’s Lifelines library to estimate engine RUL and make data-driven maintenance decisions.
Why Use Survival Analysis for Predictive Maintenance?
Survival analysis originated in healthcare for estimating patient survival times, but it can be applied to any domain where you need to predict "time-to-event." In aviation, "time-to-event" might refer to predicting the time until an engine failure or the next necessary maintenance interval. Using survival analysis for predictive maintenance provides several advantages:
- Proactive Repairs: Estimate engine lifespan to prevent unplanned downtime.
- Optimized Maintenance Intervals: Schedule maintenance based on actual usage and historical data instead of fixed intervals.
- Cost Reduction: Minimize costly reactive maintenance by intervening before critical failures.
Survival Analysis Basics: The Kaplan-Meier Estimator
The Kaplan-Meier estimator is one of the most common tools in survival analysis. It calculates the probability of survival past a given time point, accommodating censored data (cases where an event, such as failure, has not yet occurred). This is ideal for MRO teams, as they can estimate survival probabilities for engines still in service and project future maintenance needs.
Let’s dive into the code!
Step 1: Setting Up Your Environment
First, make sure you have the necessary Python packages installed. You’ll need the pandas and lifelines libraries.
pip install pandas lifelines
Step 2: Calculating Survival Probabilities with the Kaplan-Meier Estimator
We can now use the Kaplan-Meier estimator from the lifelines library to analyze the survival probabilities of the engines. This estimator will help predict the likelihood that an engine will continue to operate beyond certain hours.
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
# Instantiate the KaplanMeierFitter model
kmf = KaplanMeierFitter()
# Fit the model using the data
kmf.fit(durations=engine_df['Operating_Hours'], event_observed=engine_df['Event'])
# Plot the survival function
plt.figure(figsize=(10, 6))
kmf.plot_survival_function()
plt.title("Kaplan-Meier Survival Estimate for Engine Life")
plt.xlabel("Operating Hours")
plt.ylabel("Survival Probability")
plt.grid()
plt.show()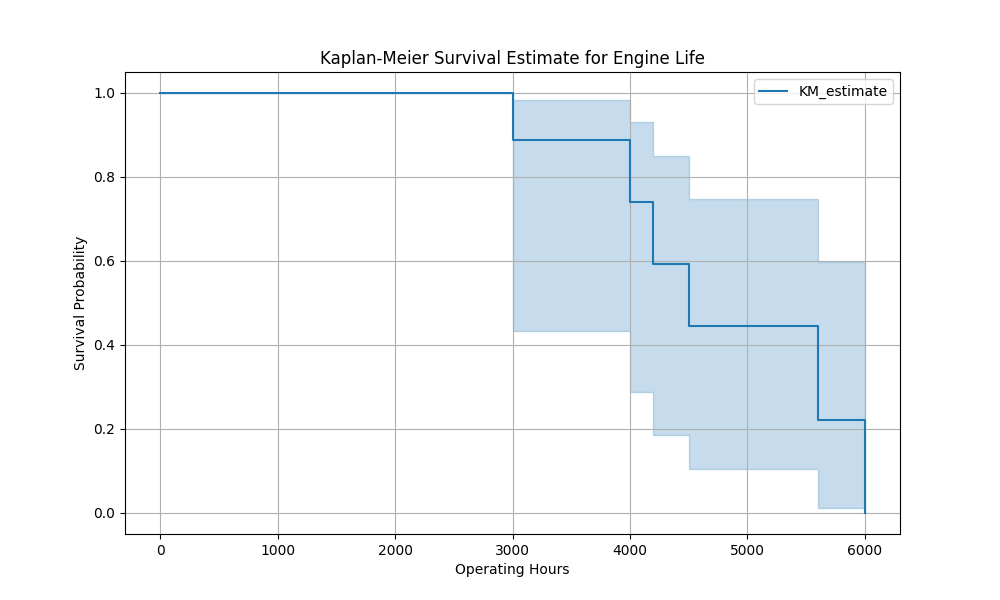
The survival function plot gives us a clear view of how the probability of survival decreases as operating hours increase. Each drop in the curve represents an observed failure, while the steady segments represent periods with no failure events.
Step 3: Interpreting the Kaplan-Meier Results
The Kaplan-Meier curve indicates the probability of an engine surviving past certain operating hours. For example, if the curve shows a survival probability of 0.8 at 3,000 hours, this means there’s an 80% chance an engine will continue running beyond 3,000 hours. These insights allow MRO teams to schedule maintenance before reaching critical failure points.
Step 4: Estimating the Mean Survival Time for Predictive Maintenance
The mean survival time provides an estimate for when most engines will require maintenance or may fail. This can guide decisions on maintenance intervals.
# Get the mean survival time (expected lifetime)
mean_survival_time = kmf.median_survival_time_
print(f"Estimated Median Survival Time: {mean_survival_time} hours")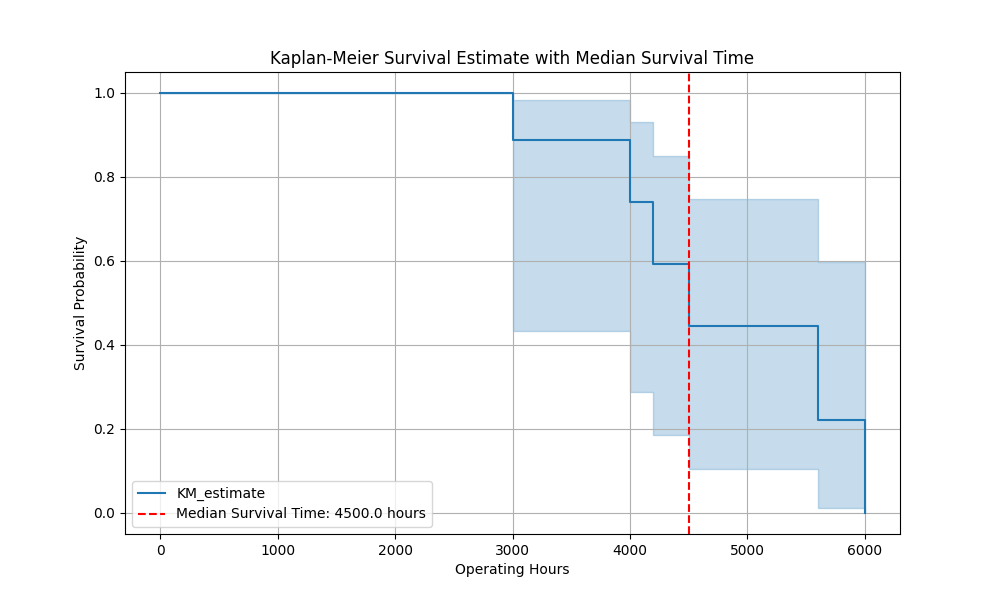
This result tells us the estimated number of operating hours after which 50% of engines are expected to require maintenance.
Step 5: Advanced Scenario – Comparing Engine Types
If your dataset contains multiple engine types, you can compare survival curves across these groups. For example, we can add a column for Engine_Type and compare the survival estimates for different types.
# Update dataset with Engine Types for comparison
engine_df['Engine_Type'] = ['A', 'A', 'B', 'B', 'A', 'A', 'B', 'B', 'A', 'B']
# Instantiate Kaplan-Meier model
kmf_a = KaplanMeierFitter()
kmf_b = KaplanMeierFitter()
# Fit and plot survival function for Engine Type A
plt.figure(figsize=(10, 6))
kmf_a.fit(engine_df[engine_df['Engine_Type'] == 'A']['Operating_Hours'],
event_observed=engine_df[engine_df['Engine_Type'] == 'A']['Event'], label='Engine Type A')
kmf_a.plot_survival_function()
# Fit and plot survival function for Engine Type B
kmf_b.fit(engine_df[engine_df['Engine_Type'] == 'B']['Operating_Hours'],
event_observed=engine_df[engine_df['Engine_Type'] == 'B']['Event'], label='Engine Type B')
kmf_b.plot_survival_function()
plt.title("Kaplan-Meier Survival Estimate by Engine Type")
plt.xlabel("Operating Hours")
plt.ylabel("Survival Probability")
plt.legend()
plt.grid()
plt.show()Comparing survival curves across engine types reveals if one type generally lasts longer than another, helping MRO teams decide on procurement, prioritizing resources, or adjusting maintenance intervals based on engine characteristics.
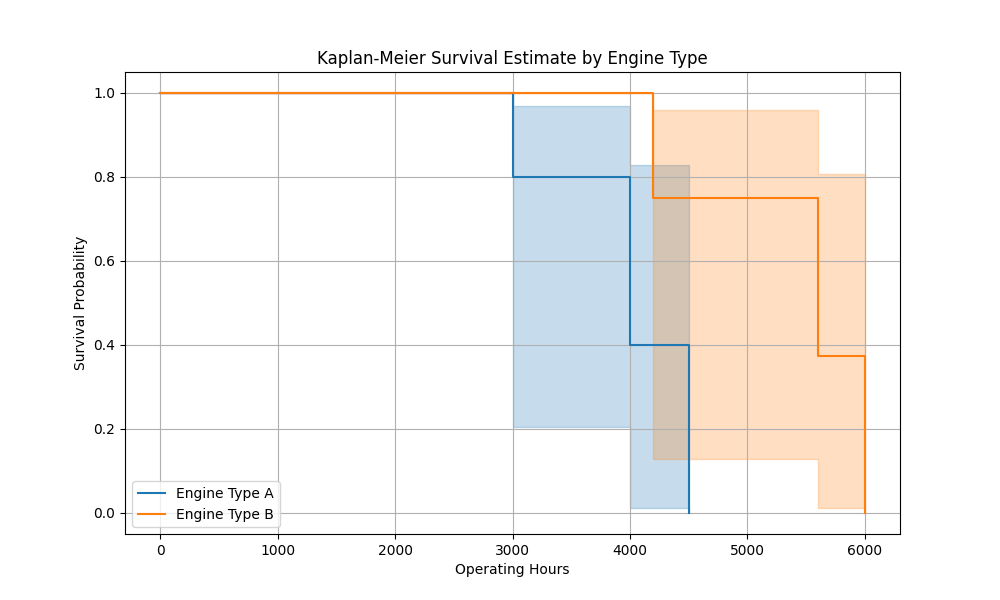
Step 6: Using Survival Analysis to Make Maintenance Recommendations
Using survival analysis, we can set maintenance intervals based on survival probabilities rather than fixed schedules. For example, if the survival probability drops significantly at 4,000 hours, maintenance could be scheduled around that time to minimize the risk of failure.
# Calculate survival probability at a specific time
time_point = 4000
survival_prob_at_time_point = kmf.predict(time_point)
print(f"Survival Probability at {time_point} operating hours: {survival_prob_at_time_point:.2f}")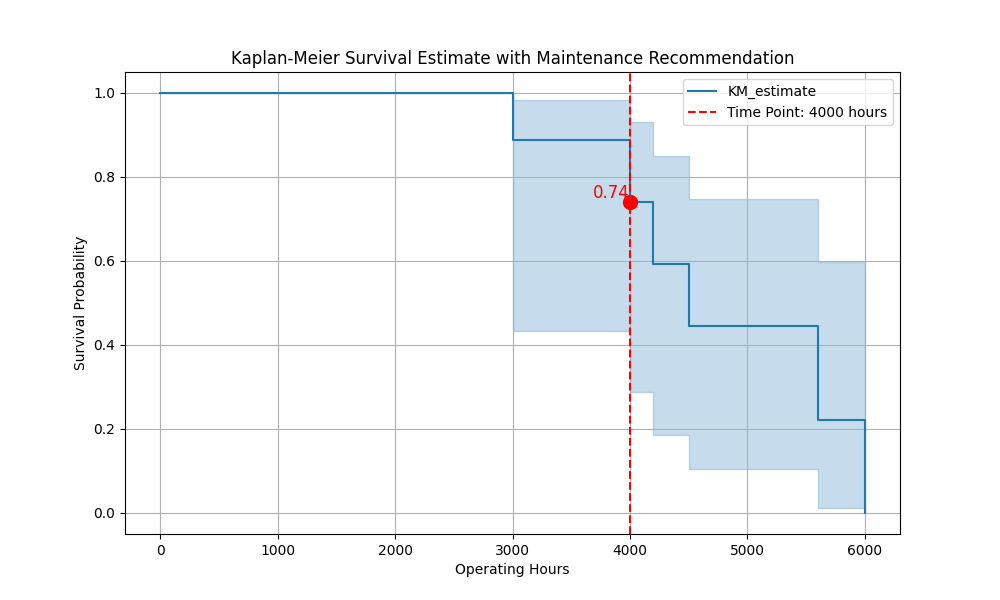
This result gives a survival probability at the specified time, helping you identify critical maintenance points. If the probability is low, maintenance should ideally occur before this threshold.
Conclusion
Survival analysis offers MRO teams powerful insights for proactive, data-driven maintenance planning. By estimating the remaining useful life of engines, we can avoid unexpected failures and optimize the timing of maintenance tasks. While we’ve shown the Kaplan-Meier estimator here, survival analysis includes more advanced techniques (like Cox proportional hazards models) for complex predictive maintenance scenarios.
Key Takeaways:
- Proactive Maintenance: Estimate engine lifespans to prevent unexpected failures.
- Data-Driven Decisions: Make maintenance decisions based on actual engine usage and survival probabilities.
- Cost Optimization: Reduce costs by avoiding reactive maintenance and optimizing parts procurement.
Predictive maintenance is a game-changer in aviation, allowing airlines and MRO teams to improve efficiency and reliability. At ePlaneAI, we specialize in leveraging advanced ML models like survival analysis to transform MRO operations and keep your aircraft in the air.


